


: 伝達関数と状態方程式
: sysconh16
: 行列指数関数と状態方程式の解
ここでは遷移行列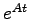 を具体的に求める方法について述べる.(2.5)式からも判るように,遷移行列
を具体的に求める方法について述べる.(2.5)式からも判るように,遷移行列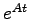 は行列の無限級数で定義される.したがって,(2.5)式から直接これを求めることは困難である.このことから,まず第1の方法としてラプラス変換を利用した求め方を紹介する.
は行列の無限級数で定義される.したがって,(2.5)式から直接これを求めることは困難である.このことから,まず第1の方法としてラプラス変換を利用した求め方を紹介する.
行列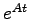 の各要素をラプラス変換して得られる行列を
の各要素をラプラス変換して得られる行列を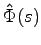 で表すことにする.すなわち
で表すことにする.すなわち
とする.(2.6)式を初期条件(2.9)の下でラプラス変換すれば
であり,関数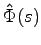 で表せば
で表せば
となる.これを整理すれば
よって
![\begin{displaymath}
e^{At} = {\cal L}^{-1}[(sI-A)^{-1}].
\end{displaymath}](img107.png) |
(3.1) |
以上により,与えられた行列 の遷移行列が(3.1)式により与えられることがわかる.
の遷移行列が(3.1)式により与えられることがわかる.
例2.3 (3.1)式を用いて,行列
に対する遷移行列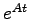 を求める.まず
を求める.まず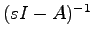 を計算すると
を計算すると
となる.したがって,上式の各要素をラプラス逆変換すると
となる.
第2の方法として,ラプラス変換を用いない方法がある.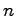 次正方行列
次正方行列 の相異なる固有値を
の相異なる固有値を
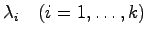 とし,各
とし,各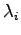 の重複度を
の重複度を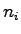 とする.明らかに
とする.明らかに
が成り立つ.したがって,行列 の特性多項式
の特性多項式
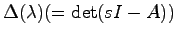 は
は
で与えられる.ただし,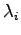 は
は の相異なる固有値で,
の相異なる固有値で,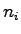 はその重複度を表し,
はその重複度を表し,
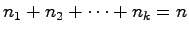 である.
これに対し、時間
である.
これに対し、時間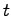 の関数
の関数
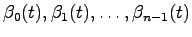 を係数として
を係数として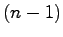 次多項式
次多項式
を考えると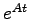 は
は
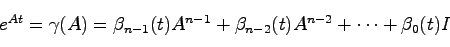 |
(3.2) |
によって与えられる.ただし
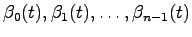 は,
は,
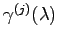 を
を
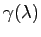 の
の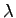 に関する
に関する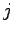 階微係数とするとき,次式を満足するものとする.
階微係数とするとき,次式を満足するものとする.
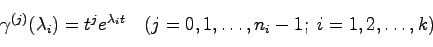 |
(3.3) |
実際,(3.2)式により行列指数関数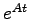 が与えられることを示す.
が与えられることを示す.
任意の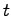 に対して関数
に対して関数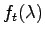 を
を
で定義する.上式を両辺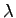 についての
についての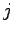 階導関数を求めると
階導関数を求めると
を得る.これと(3.3)式より
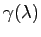 と
と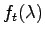 に対し
に対し
が成り立つ.したがって,
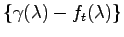 は,
は,
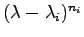 を因数として持つ.ゆえに
を因数として持つ.ゆえに
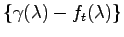 は,
は, の特性多項式
の特性多項式
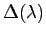 を因数として持つ.さらにケーリー・ハミルトンの定理より
を因数として持つ.さらにケーリー・ハミルトンの定理より
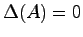 であるから
であるから
よって
となる.
例2.4 (3.2)式を用いて行列
に対する行列指数関数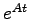 を求めてみる.
を求めてみる.
より,特性多項式は
となる.したがって, の固有値とその重複度は
の固有値とその重複度は
である.行列 は3次正方行列であるから
は3次正方行列であるから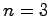 .すなわち,
.すなわち,
とおくと,(3.3)式より
となる.また,(3.2)式より
となる.したがって,(3.4)〜(3.7)式より,
となる.



: 伝達関数と状態方程式
: sysconh16
: 行列指数関数と状態方程式の解
endo
平成16年6月30日
![]() の各要素をラプラス変換して得られる行列を
の各要素をラプラス変換して得られる行列を![]() で表すことにする.すなわち
で表すことにする.すなわち
![\begin{displaymath}
{\cal L}\left[ \frac{d}{dt}e^{At} \right] = {\cal L} \left[ Ae^{At} \right]
\end{displaymath}](img104.png)
![]() の遷移行列が(3.1)式により与えられることがわかる.
の遷移行列が(3.1)式により与えられることがわかる.
![\begin{displaymath}
A = \left[ \begin{array}{cc} -1 & 0 1 & -2 \end{array} \right]
\end{displaymath}](img108.png)
![\begin{eqnarray*}
(sI-A)^{-1} &=& \left[ \begin{array}{cc} s+1 & 0 -1 & s+2 \...
...cc} 1/(s+1) & 0 1/(s+1)-1/(s+2) & 1/(s+2) \end{array} \right]
\end{eqnarray*}](img110.png)
![\begin{displaymath}
e^{At} = \left[ \begin{array}{cc} e^{-t} & 0 e^{-t}-e^{-2t} & e^{-2t}
\end{array} \right]
\end{displaymath}](img111.png)
![]() 次正方行列
次正方行列![]() の相異なる固有値を
の相異なる固有値を
![]() とし,各
とし,各![]() の重複度を
の重複度を![]() とする.明らかに
とする.明らかに
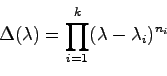
![]() が与えられることを示す.
が与えられることを示す.
![]() に対して関数
に対して関数![]() を
を
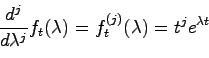
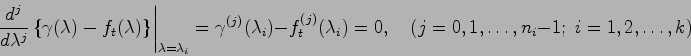
![\begin{displaymath}
A = \left[ \begin{array}{ccc} -1 & 1 & 0 0 & -1 & 0 0 & -1 & -2
\end{array} \right]
\end{displaymath}](img138.png)
![\begin{displaymath}
sI-A = \left[ \begin{array}{ccc} s+1 & -1 & 0 0 & s+1 & 0 \\
0 & 1 & s+2 \end{array} \right]
\end{displaymath}](img139.png)
![\begin{displaymath}
e^{At} = \left[ \begin{array}{ccc}
e^{-t} & te^{-t} & 0 \\
...
...e^{-t} & 0 \\
0 & e^{-2t}-e^{-t} & e^{-2t}
\end{array}\right]
\end{displaymath}](img154.png)