フルビッツの安定条件

定理5.1では安定性判別の必要十分条件はシステムの極の実部がすべて負であることであった．しかし一般に高次元のシステムではシステムの極を求めること自体が困難である場合が多い．したがって定理5.1の方法でシステムの内部安定性を求めることは現実的ではない．このことから，本節ではシステムの極を求めることなしに安定性を判別する方法（フルビッツの安定条件）を示す．

いま任意の$n$次実係数代数方程式

$$a_0 s^n + a_1 s^{n-1} + \cdots + a_n = 0$$ (16.1)

を考える．ただし$a_0>0$と仮定する．(5.19)式の左辺を$f(s)$とおき，(5.19)式の根の実部がすべて負であるとき$f(s)$は，フルビッツ多項式であるということにする．

 

定理5.2　$a_0>0$のもとに$f(s)$がフルビッツ多項式であるためには， $a_1,a_2,\ldots,a_n$がすべて正でなければならない．

 

証明　$f(s)$がフルビッツ多項式であるとすると，(5.19)式の根は， $-\alpha_j,\; j=1,2, \ldots, n_r$および $-\beta_k \pm i \gamma_k, \; k = 1,2,\ldots, n_c$で与えられる．ただし，各 $\alpha_j,\beta_k$および$\gamma_k$は正の実数であり， $n_r + 2 n_c = n$である．このとき

$$\begin{eqnarray*} f(s) &=& a_0 \prod_{j=1}^{n_r}(s+\alpha_j) \prod_{k=1}^{n_c}(s... ...\alpha_j) \prod_{k=1}^{n_c}(s^2+2\beta_ks+\beta_k^2 +\gamma_k^2) \end{eqnarray*}$$

であり，したがって上式右辺を展開したときの係数である $a_0,a_1,a_2,\ldots,a_n$はすべて正である．

 

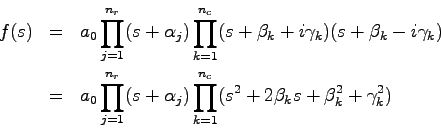
上の定理5.2の逆は成立しない．すなわち， $a_0,a_1,a_2,\ldots,a_n$がすべて正であっても$f(s)$はフルビッツ多項式になるとは限らない．このことに対する反例はすぐに見つかる．（例えば$s^3+s^2+s+6$が教科書にある．）そこで，次に$f(s)$がフルビッツ多項式であるための必要十分条件を与える．いま，(5.19)式に対して$n\times n$行列$H$を

$$H = \left[ \begin{array}{cccccc} a_1 & a_3 & a_5 & a_7 & \cd... ...\\ 0 & 0 & \cdots & \cdots & \cdots & a_n \end{array}\right]$$ (16.2)

で定義する．ただし$j > n$に対しては$a_j = 0$とする．行列$H$はフルビッツ行列と呼ばれる．$H$の各行が(5.19)式の係数$a_j$を１つおきに取ったものとなっていること，及び対角要素が $a_1,a_2,\ldots,a_n$であることに注意する．フルビッツ行列の$i \times i$主座小行列の行列式の値を$\Delta_i$とする．すなわち

$$\Delta_1 = a_1, \quad \Delta_2 = \left[ \begin{array}{cc} a_... ... a_0 & a_2 \end{array}\right], \ldots, \quad \Delta_n = \det H$$

とする．このとき次の定理が成り立つ．

 

定理5.3　（フルビッツの安定条件）$a_0>0$のもとに$f(s)$がフルビッツ多項式であるための必要十分条件は

$$\Delta_i > 0, \quad i = 1,2,\ldots, n$$ (16.3)

を満足することである．

 

証明は時間の関係上省略する.

古典制御理論においては，通常図5.3のような１入力１出力システムの安定性を判別するために，特性方程式

$$1 + G(s) = 0$$

に対してフルビッツの安定条件を適用していた．これに対し，ここでは定理5.1の結果に基づいて，行列$A$の特性方程式に適用することにより，システム(5.1)の漸近安定性を判別する．

 

例5.4　システム

$$\dot{x} = Ax, \quad A = \left[ \begin{array}{cccc} 0 & 1 & 0... ... & 1 \\ 0 & 0 & -1 & 0 \\ 0 & -2 & 0 & -3 \end{array}\right]$$

の安定性をフルビッツの安定性により調べる．

$$(sI-A) = \left[ \begin{array}{cccc}s & -1 & 0 & 0 \\ 1 & s ... ...-1 \\ 0 & 0 & s+1 & 0 \\ 0 & 2 & 0 & s+3 \end{array}\right]$$

より

$$\Delta(s) = \det(sI-A) = s^4 + 4s^3 + 6s^2 + 6s + 3$$

となり， $n=4, a_0 = 1 > 0$であり， $a_1 = 4, a_2 = 6, a_3 = 6, a_4 = 3$ であるから

$$H = \left[ \begin{array}{cccc} 4 & 6 & 0 & 0 \\ 1 & 6 & 3 & 0 \\ 0 & 4 & 6 & 0 \\ 0 & 1 & 6 & 3 \end{array}\right]$$

となり，

$$\Delta_1 = a_1 = 4 > 0, \quad \Delta_2 = \left\vert \begin{a... ... 0 \\ 1 & 6 & 3 \\ 0 & 4 & 6 \end{array}\right\vert = 60 > 0$$

となる．さらに $\Delta_4 = a_4 \Delta_3 > 0$となり，このシステムが漸近安定であることがわかる．

 

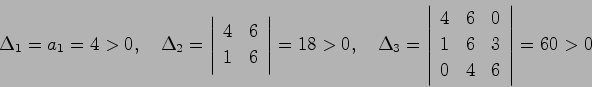
なお，計算量の点からは，定理5.3よりもその変形である次の定理が優れている．

 

定理5.4　$a_0>0$のもとに$f(s)$がフルビッツ多項式であるための必要十分条件は，次の２条件が成立することである．

1. $a_1,a_2,\ldots,a_n$がすべて正である．
2. 次のいずれかが成立する．

この定理を適用する場合，まず条件1.を調べ，これが満たされていなければシステムは安定ではない．条件1.が満たされている場合のみ条件2.を調べる．$n$が偶数ならば2.(b)を用いれば計算量がより少なくてすむ．例えば例5.4の場合には， $a_i > 0,\; i = 1,2,3,4$，より条件1.が満たされており，$n=4$から2.(b)をとって$\Delta_3$の値のみをしれべればよく，$\Delta_2$の計算は必要ない．