


: 可観測性
: sysconh16
: 伝達関数と状態方程式
本節では,与えられたシステムに対し,システムの状態を,任意の初期状態から有限時間内に0状態へ導くことができるか(可制御性)について考察する.すなわち与えられたシステムが何らかの原因で暴走を始めたような場合に適当な入力によりシステムを停止状態にできるか否かについて考える。
まず,可制御性の定義から始める.
[可制御性] 任意の初期時刻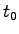 と,システムの任意の初期状態
と,システムの任意の初期状態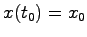 が
与えられたとき,適当な有限時刻
が
与えられたとき,適当な有限時刻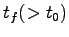 まで適当な入力
まで適当な入力
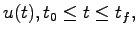 を加えることによって,
を加えることによって,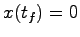 とすることができるならば,このシステムは可制御であるという.
とすることができるならば,このシステムは可制御であるという.
可制御性の判定条件にはいくつかあるが,最も一般的なものとして次の可制御性行列
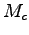 を利用した判定条件が挙げられる.
を利用した判定条件が挙げられる.
定理 (可制御性の判定規範)次の状態方程式で記述されるシステムを考える.
ただし,係数行列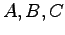 はそれぞれ
はそれぞれ
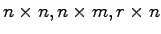 定数行列とする.
定数行列とする.
このシステム(5.1),(5.2)が可制御であるための必要十分条件は
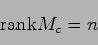 |
(5.3) |
となることである.ここで,可制御性行列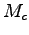 は以下の式で定義される
は以下の式で定義される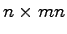 行列である.
行列である.
![\begin{displaymath}
M_c = \left[ \begin{array}{cccc} B & AB & \cdots & A^{n-1}B \end{array}\right]
\end{displaymath}](img202.png) |
(5.4) |
上記の定理の証明は後回しにして、いくつか簡単な例により可制御性について調べることにする。
例3.1 システム
![\begin{displaymath}
\dot{x}(t) = \left[ \begin{array}{cc}0 & 0 0 & -1 \end{ar...
...x(t)
+ \left[ \begin{array}{c} 1 1 \end{array} \right] u(t)
\end{displaymath}](img203.png) |
(5.5) |
を考える.システム(5.5)に対する可制御性行列は
となり,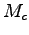 を変形すると
を変形すると
となり,
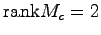 であるから,このシステムは可制御である.
であるから,このシステムは可制御である.
次に,このシステムについて,ブロック線図を考えてみる.適当な平行移動によって初期状態を0とすると
より,ラプラス変換によって
となる.したがってブロック線図は教科書の図3.1になり,状態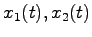 は入力
は入力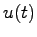 に
依存して変化することがわかる.これにより入力をうまく選べば平行移動前の状態を0状態に
することが可能と考えられる。(実際には上式から状態量を任意の値に移動できることを示すか、
平行移動前の状態を0状態にするための具体的な入力を求める必要がある。)
に
依存して変化することがわかる.これにより入力をうまく選べば平行移動前の状態を0状態に
することが可能と考えられる。(実際には上式から状態量を任意の値に移動できることを示すか、
平行移動前の状態を0状態にするための具体的な入力を求める必要がある。)
例3.2 システム
![\begin{displaymath}
\dot{x}(t) = \left[ \begin{array}{cc}0 & 0 0 & -1 \end{ar...
...]x(t)
+ \left[ \begin{array}{c}1 0 \end{array} \right] u(t)
\end{displaymath}](img209.png) |
(5.6) |
を考える.システム(5.6)に対する可制御性行列は
となり,
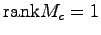 であるから,このシステムは可制御でない.
であるから,このシステムは可制御でない.
次に,このシステムについて,ブロック線図を考えてみる.前例同様、適当な平行移動により初期状態を0とすると
より,ラプラス変換によって
となる.したがってブロック線図は教科書の図3.2になり,状態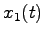 は入力
は入力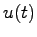 に依存しているものの,状態
に依存しているものの,状態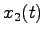 は入力
は入力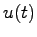 に依存していないことがわかる.
に依存していないことがわかる.
例3.3 システム
![\begin{displaymath}
\dot{x}(t) = \left[ \begin{array}{cc}-1 & 0 0 & -1 \end{a...
...]x(t)
+ \left[ \begin{array}{c}1 1 \end{array} \right] u(t)
\end{displaymath}](img214.png) |
(5.7) |
を考える.システム(5.7)に対する可制御性行列は
となり,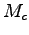 を変形すると
を変形すると
となり,
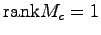 であるから,このシステムは可制御でない.
であるから,このシステムは可制御でない.
次に,このシステムについて,ブロック線図を考えてみる.適当な平行移動により初期状態を0とすると
より,ラプラス変換によって
となる.したがってブロック線図は教科書の図3.3になる.これによると,状態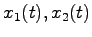 が入力
が入力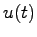 に依存しているから可制御と考えられるが,上で示したように実際には可制御でない.何故か?
に依存しているから可制御と考えられるが,上で示したように実際には可制御でない.何故か?
このことを考察するため(5.8),(5.9)を再度確認すると,これらが一致していることがわかる.さらに状態方程式における状態の取り方は任意であったことから,システム(5.7)の状態を新たに
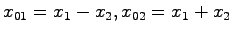 と取り直すと,
と取り直すと,
より,システムは次のようになる.
したがって,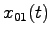 は入力に無関係になり,可制御ではない.
は入力に無関係になり,可制御ではない.
定理の証明 まず必要性を示す。すなわちシステム(5.2)が可制御であると仮定すると条件(5.3)が成り立つことを示す。
システム(5.2),(5.3)が可制御であるとする.
初期時刻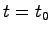 における初期条件を
における初期条件を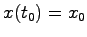 とすると,(5.2)式の解は
とすると,(5.2)式の解は
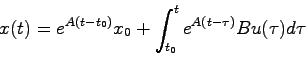 |
(5.12) |
となる.これに対し,可制御性の仮定から,任意の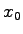 に対して,適当な終端時刻
に対して,適当な終端時刻
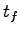 と入力
と入力
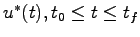 が存在して,この入力により
が存在して,この入力により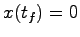 と
なるから
と
なるから
すなわち,
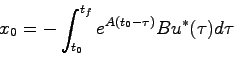 |
(5.13) |
となる.ここで行列指数関数の固有値による導出法を思い出せば、行列指数関数が有限の多項式により
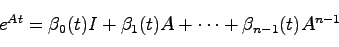 |
(5.14) |
と表せるはずであった.ただし,各
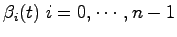 は適当なスカラ関数である.
(5.14)式を(5.13)式に代入すると,,各
は適当なスカラ関数である.
(5.14)式を(5.13)式に代入すると,,各
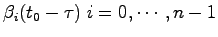 がスカラ値であることに注意すれば
がスカラ値であることに注意すれば
となり,簡単のため
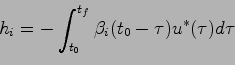 |
(5.15) |
と置くと,(5.13),(5.14),(5.15)式より
となる.システムは可制御であるから、左辺の初期値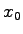 (
(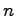 次ベクトル)がどんな値をとったとしても、それと右辺が等しくなるように
次ベクトル)がどんな値をとったとしても、それと右辺が等しくなるように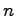 次ベクトル
次ベクトル
![$\left[ \begin{array}{cccc}h_0^T & h_1^T \cdots h_{n-1}^T \end{array}\right]^T$](img241.png) を設定できなければならない。
を設定できなければならない。
このことは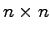 行列
行列
![$M_c = \left[ \begin{array}{cccc}B & AB & \cdots & A^{n-1}B \end{array}\right]$](img243.png) が
が
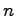 次元空間
次元空間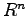 から
から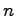 次元空間
次元空間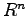 への線形写像になっていることを考えると
への線形写像になっていることを考えると
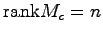 でなければならない。すなわち(5.3)式が満たされることを示している.
でなければならない。すなわち(5.3)式が満たされることを示している.
次に十分性について証明する。すなわち条件(5.3)が成り立つと仮定すると、状態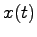 を有限時間内に
を有限時間内に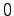 にする入力
にする入力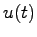 が具体的に構成できることを示す。
が具体的に構成できることを示す。
必要性の証明と同様に、初期時刻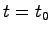 で初期状態
で初期状態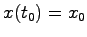 に対する状態方程式の解は
に対する状態方程式の解は
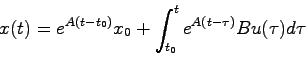 |
(5.16) |
である。ここで状態がある時刻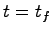 において
において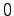 になるためには
になるためには
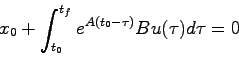 |
(5.17) |
である必要がある。入力の候補を考えるため上式(5.17)の左辺第2項を考えると、被積分関数が
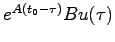 であることから、もっとも単純な方法として
であることから、もっとも単純な方法として
![$u(\tau)= - \left[ e^{A(t_0-\tau)}B \right]^{-1}x_0 \times \alpha $](img250.png) を考えればよさそうである(
を考えればよさそうである(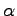 は適当な定数)が、
は適当な定数)が、
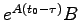 が正方行列になるとは限らないのでこのままでは逆行列が取れるかもわからない。そのため少なくとも正方行列を保障するため
が正方行列になるとは限らないのでこのままでは逆行列が取れるかもわからない。そのため少なくとも正方行列を保障するため
として(5.17)式に代入すると
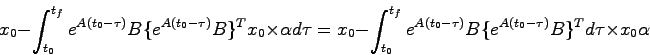 |
(5.18) |
となり、右辺第2項の定積分は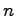 次正方行列であるから
次正方行列であるから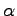 としてこの逆行列を指定すれば
としてこの逆行列を指定すれば
となる。
以上より入力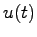 の候補としては、(5.17)より
の候補としては、(5.17)より
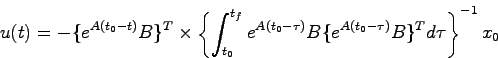 |
(5.19) |
を考える。表現を簡単にするため
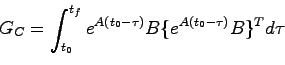 |
(5.20) |
とすると
となる。これにより形式的には有限時間内に状態を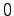 にする入力が求められた。
にする入力が求められた。
しかしながら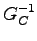 の存在性(
の存在性(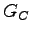 の正則性)については触れていないので、以下これを考察する。
の正則性)については触れていないので、以下これを考察する。
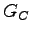 は実対称行列であるから次の定理が利用できる。
は実対称行列であるから次の定理が利用できる。
(定理)実対称行列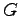 の全ての主小行列式が正であるための必要十分条件は
の全ての主小行列式が正であるための必要十分条件は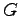 が正定行列である。
が正定行列である。
上記の定理から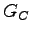 が正則である(行列式が
が正則である(行列式が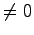 である)ためには正定であればよいことがわかる。幸い
である)ためには正定であればよいことがわかる。幸い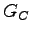 以下のようにして準正定であることが判っているから
以下のようにして準正定であることが判っているから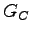 が正定であるための条件を求める。
が正定であるための条件を求める。
実は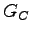 を構成する時点で上の定理に照らし合わせ準正定であるような
を構成する時点で上の定理に照らし合わせ準正定であるような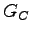 を求めている!
を求めている!
任意のベクトル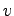 について
について
となるから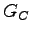 は準正定である。いま、
は準正定である。いま、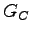 が正定でないとすると、適当な
が正定でないとすると、適当な
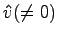 に対して
に対して
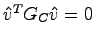 が成立し
が成立し
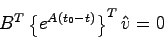 |
(5.21) |
でなければならない。これを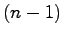 回まで微分すると
回まで微分すると
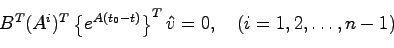 |
(5.22) |
を得る。(16.3)と(17.1)をまとめると
となる。指数関数行列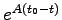 は正則であるから、可制御性の条件
は正則であるから、可制御性の条件
が成り立つ場合には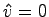 でなければならず、これは
でなければならず、これは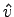 の取り方に矛盾する。以上により十分性が示された。
の取り方に矛盾する。以上により十分性が示された。



: 可観測性
: sysconh16
: 伝達関数と状態方程式
endo
平成16年6月30日
![]() と,システムの任意の初期状態
と,システムの任意の初期状態![]() が
与えられたとき,適当な有限時刻
が
与えられたとき,適当な有限時刻![]() まで適当な入力
まで適当な入力
![]() を加えることによって,
を加えることによって,![]() とすることができるならば,このシステムは可制御であるという.
とすることができるならば,このシステムは可制御であるという.
![]() を利用した判定条件が挙げられる.
を利用した判定条件が挙げられる.
![\begin{displaymath}
M_c = \left[ \begin{array}{cc} B & AB \end{array}\right]
= \left[ \begin{array}{cc} 1 & 0 1 & -1 \end{array}\right]
\end{displaymath}](img204.png)
![\begin{displaymath}
\left[ \begin{array}{cc} 1 & 0 1 & -1 \end{array}\right]
...
...ow
\left[ \begin{array}{cc} 1 & 0 0 & -1 \end{array}\right]
\end{displaymath}](img205.png)
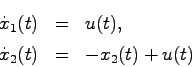
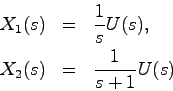
![\begin{displaymath}
M_c = \left[ \begin{array}{cc} B & AB \end{array}\right]
= \left[ \begin{array}{cc} 1 & 0 0 & 0 \end{array}\right]
\end{displaymath}](img210.png)
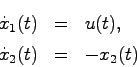
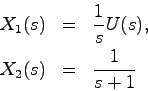
![\begin{displaymath}
M_c = \left[ \begin{array}{cc} B & AB \end{array}\right]
= \left[ \begin{array}{cc} 1 & -1 1 & -1 \end{array}\right]
\end{displaymath}](img215.png)
![\begin{displaymath}
\left[ \begin{array}{cc} 1 & -1 1 & -1 \end{array}\right]...
...ow
\left[ \begin{array}{cc} 1 & -1 0 & 0 \end{array}\right]
\end{displaymath}](img216.png)
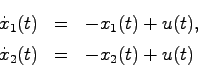
![]() と取り直すと,
と取り直すと,
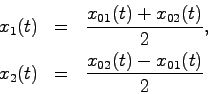
![]() における初期条件を
における初期条件を![]() とすると,(5.2)式の解は
とすると,(5.2)式の解は
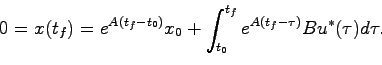
![\begin{eqnarray*}
x_0 &=& Bh_0 + ABh_1 + \cdots + A^{n-1}Bh_{n-1} \\
&=& \left[...
...{array}{cccc}h_0^T & h_1^T \cdots h_{n-1}^T \end{array}\right]^T
\end{eqnarray*}](img240.png)
![$\left[ \begin{array}{cccc}h_0^T & h_1^T \cdots h_{n-1}^T \end{array}\right]^T$](img241.png) を設定できなければならない。
を設定できなければならない。
![]() 行列
行列
![$M_c = \left[ \begin{array}{cccc}B & AB & \cdots & A^{n-1}B \end{array}\right]$](img243.png) が
が
![]() 次元空間
次元空間![]() から
から![]() 次元空間
次元空間![]() への線形写像になっていることを考えると
への線形写像になっていることを考えると
![]() でなければならない。すなわち(5.3)式が満たされることを示している.
でなければならない。すなわち(5.3)式が満たされることを示している.
![]() を有限時間内に
を有限時間内に![]() にする入力
にする入力![]() が具体的に構成できることを示す。
が具体的に構成できることを示す。
![]() で初期状態
で初期状態![]() に対する状態方程式の解は
に対する状態方程式の解は
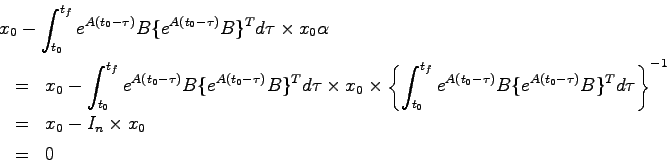
![]() の候補としては、(5.17)より
の候補としては、(5.17)より
![]() の存在性(
の存在性(![]() の正則性)については触れていないので、以下これを考察する。
の正則性)については触れていないので、以下これを考察する。
![]() は実対称行列であるから次の定理が利用できる。
は実対称行列であるから次の定理が利用できる。
の全ての主小行列式が正であるための必要十分条件は
が正定行列である。
![]() が正則である(行列式が
が正則である(行列式が![]() である)ためには正定であればよいことがわかる。幸い
である)ためには正定であればよいことがわかる。幸い![]() 以下のようにして準正定であることが判っているから
以下のようにして準正定であることが判っているから![]() が正定であるための条件を求める。
が正定であるための条件を求める。
を構成する時点で上の定理に照らし合わせ準正定であるような
を求めている!
![]() について
について
![\begin{eqnarray*}
v^T G_C v &=& \int_{t_0}^{t_f} v^T e^{A(t_0-\tau)}B \{ e^{A(t_...
...t[ B^T \left\{ e^{A(t_0-\tau)} \right\}^T v \right] d\tau \geq 0
\end{eqnarray*}](img264.png)
![\begin{displaymath}
\left[ \begin{array}{cccc}B & AB & \cdots & A^{n-1}B
\end{array} \right]^T \left\{ e^{A(t_0-t)}\right\}^T \hat{v} = 0
\end{displaymath}](img269.png)