


: 状態フィードバックによる多入力システムの極配置
: sysconh16
: 状態フィードバックによる極配置問題
本節では1入力で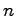 次元状態変数をもつシステム
次元状態変数をもつシステム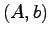 ,すなわち
,すなわち
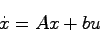 |
(21.1) |
の極配置問題を考える.
定理6.1 1入力システム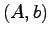 が可制御であれば,状態フィードバック
が可制御であれば,状態フィードバック
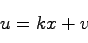 |
(21.2) |
によって任意の極は位置が可能である.ただし,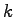 は状態フィードバックゲインを
表す
は状態フィードバックゲインを
表す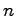 次元横ベクトルである.
次元横ベクトルである.
証明 配置したい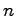 個の極の集合を
個の極の集合を
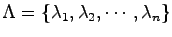 とする.状態フィードバック(21.2)によって得られる
閉ループシステムは,
とする.状態フィードバック(21.2)によって得られる
閉ループシステムは,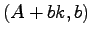 であるから,行列
であるから,行列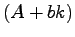 の特性多項式が
の特性多項式が
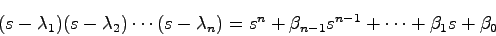 |
(21.3) |
に一致するような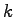 が存在するならば,希望の極配置が可能ということになる.
が存在するならば,希望の極配置が可能ということになる.
さて対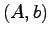 が可制御であると仮定していることから,適当な正則行列
が可制御であると仮定していることから,適当な正則行列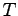 を用いて
次のような可制御正準形
を用いて
次のような可制御正準形
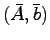 に変形できる:
に変形できる:
ここで,
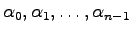 は
は の特性多項式
の特性多項式
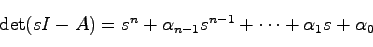 |
(21.4) |
の係数である.このとき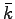 を
を
![\begin{displaymath}
\bar{k} = \left[ \begin{array}{cccc}
\alpha_0-\beta_0 & \alp...
...\beta_1 & \ldots & \alpha_{n-1}-\beta_{n-1}
\end{array}\right]
\end{displaymath}](img940.png) |
(21.5) |
とおき,さらに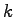 を
を
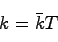 |
(21.6) |
とおけば
であるから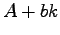 の特性方程式は(21.3)式に一致する.よって,任意の極は位置が可能であることが示された.
の特性方程式は(21.3)式に一致する.よって,任意の極は位置が可能であることが示された.
詳細は次節で述べるが,定理6.1の仮定"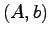 が可制御対"は任意の極配置が可能であるための必要条件となっている.
が可制御対"は任意の極配置が可能であるための必要条件となっている.
また,(21.6)式の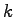 は
は
により求めることもできる.これをAckermanのアルゴリズムという(証明略).



: 状態フィードバックによる多入力システムの極配置
: sysconh16
: 状態フィードバックによる極配置問題
endo
平成16年6月30日
![]() が可制御であれば,状態フィードバック
が可制御であれば,状態フィードバック
![]() 個の極の集合を
個の極の集合を
![]() とする.状態フィードバック(21.2)によって得られる
閉ループシステムは,
とする.状態フィードバック(21.2)によって得られる
閉ループシステムは,![]() であるから,行列
であるから,行列![]() の特性多項式が
の特性多項式が
![]() が可制御であると仮定していることから,適当な正則行列
が可制御であると仮定していることから,適当な正則行列![]() を用いて
次のような可制御正準形
を用いて
次のような可制御正準形
![]() に変形できる:
に変形できる:
![\begin{displaymath}
\bar{A} = TAT^{-1} = \left[ \begin{array}{ccccc}
0 & 1 & 0 &...
...n{array}{c}
0 \vdots \vdots 0 1
\end{array}\right]
\end{displaymath}](img936.png)
![\begin{eqnarray*}
A + bk &=& T^{-1}(\bar{A}+\bar{b}\bar{k})T \\
\bar{A} + \bar{...
...& -\beta_1 & -\beta_2 & \cdots & -\beta_{n-1}
\end{array}\right]
\end{eqnarray*}](img942.png)
![]() が可制御対"は任意の極配置が可能であるための必要条件となっている.
が可制御対"は任意の極配置が可能であるための必要条件となっている.
![]() は
は