状態フィードバックによる多入力システムの極配置

本節では，前節の結果を一般化して，多入力システムにおいて，システムが可制御であることが，状態フィードバックによって任意の極配置が可能であるための必要十分条件であることを示す．

 

定理6.2　システム(20.1)が，状態フィードバック(20.3)によって（実軸について対称な範囲で）任意の極配置が可能なための必要十分条件は，対$(A,B)$が可制御なことである．

 

（証明）　十分性を示す．

システム(20.1)が可制御であれば，定理3.6により，対$(A,B)$を適当な同値変換$T$を用いて可制御正準形 $(\bar{A},\bar{B})$に変換できる．以下では表示の簡単のため，$m=2$（２入力）で可制御性指数が $\mu_1 = 3,\mu_2=2$の場合についてのみ証明を行なう．ただし，一般の$m$及び $\mu_1,\mu_2,\ldots, \mu_m$の場合にも全く同様に証明できる．

$\mu_1 = 3,\mu_2=2$より， $\bar{A},\bar{B}$は教科書p.51より

$$\bar{A} = \left[ \begin{array}{ccc\vert cc} 0 & 1 & 0 & 0 & ... ... 1 & \bar{b}_{32} \\ \hline 0 & 0 0 & 1 \end{array}\right]$$

となる．いま，配置したい極の集合 $\Lambda=\{\lambda_1,\lambda_2,\ldots, \lambda_5\}$から(21.3)式：

$$(s-\lambda_1)(s-\lambda_2)\cdots(s-\lambda_n) = s^n + \beta_{n-1}s^{n-1}+ \cdots + \beta_1 s + \beta_0$$

によって $\beta_0,\beta_1,\ldots, \beta_4$を定める．このとき，状態フィードバック制御則

$$\begin{eqnarray*} u &=& \bar{K}\bar{x}+v, \\ \bar{K} &=& \left[ \begin{array}{c... ...eta_0 & \beta_1 & \beta_2 & \beta_3 & \beta_4 \end{array}\right] \end{eqnarray*}$$

を用いると

$$\bar{A}+\bar{B}\bar{K} = \left[ \begin{array}{ccccc} 0 & 1 &... ...& -\beta_1 & -\beta_2 & -\beta_3 & -\beta_4 \end{array}\right]$$

となるから，望みの極配置が確かに実現できる． なお，もとのシステム$(A.B)$に対しては，定理6.1の証明と同様に$K=\bar{K}T$とおけばよい．

必要性の証明は省略する．

 

多入力システムに対する極配置のための状態フィードバック則を求める１つの方法は，上の定理の十分性の証明で用いた方法である．すなわち，適当な同値変換$\bar{x}=Tx$によって可制御正準形 $(\bar{A},\bar{B})$に変換した後，希望の極配置を実現するための状態フィードバックゲイン$\bar{K}$を求め，最後に逆変換$K=\bar{K}T$によって，もとのシステムに対する状態フィードバック制御則$u=Kx+v$を定める．

 

例6.3　例3.7のシステム，すなわち$A,B$が

$$A = \left[ \begin{array}{ccccc} 1 & 0 & 1 & 0 & 1 \\ 0 & 0 ... ... 0 & 0 1 & 0 0 & 1 1 & 0 0 & -1 \end{array}\right]$$

で与えられるシステム$(A,B)$に対して，極を $\{-1,-1,-2,-1\pm j\}$に設定する状態フィードバック則を求める．まず例3.8より，このシステムの可制御正準形 $(\bar{A},\bar{B})$及び変換行列$T$は

$$\bar{A} = \left[ \begin{array}{ccc\vert cc} 0 & 1 & 0 & 0 & ... ...2 & 1 & -1 & -1 & -1 \\ 3 & 0 & 0 & 0 & -1 \end{array}\right]$$

であり，また，(21.3)式より

$$(s+1)^2(s+2)(s^2+2s+2) = s^5+6s^4+15s^3+20s^2+14s+4$$

となるから $\beta_0 = 4, \beta_1 = 14, \beta_2 = 20, \beta_3 = 15, \beta_4 = 6$ となる．したがって，これと$\bar{A}$から，

$$\begin{eqnarray*} \bar{k}_2 &=& \left[ \begin{array}{ccccc} -8 & -16 & -20 & -15... ...begin{array}{ccccc} -8 & -14 & -22 & -14 & -5 \end{array}\right] \end{eqnarray*}$$

となり

$$\bar{K} = \left[ \begin{array}{ccccc} -8 & -14 & -22 & -14 & -5 \\ -8 & -16 & -20 & -15 & -5 \end{array}\right]$$

となる．よって状態フィードバックゲイン$K$は以下のようになる．

$$K = \bar{K}T = \left[ \begin{array}{ccccc} -65 & -36 & -44 & 14 & -61 \\ -69 & -35 & -41 & 15 & -56 \end{array}\right]$$

極配置のための状態フィードバック則を求めるもう1つの方法として，疋田らの方法がある．これは希望する極配置の与え方に少し制約があるが，計算が容易な方法である． 以下にこれを説明する．

 

疋田の方法　希望する極 $\Lambda = \{ \lambda_1, \lambda_2, \ldots, \lambda_n\}$が，もとのシステムの極（$A$の固有値）を含まず，入力の次元$m$に対して$m$重極を越える重複極はもたないという制約を満たすものとする．

• $\Lambda$がすべて実数極である場合
  1. 適当に$m$次元ベクトル $\xi_i, \; i = 1,2,\ldots,$を選び
     

     $$v_i = (A-\lambda_iI)^{-1}B\xi_i$$ (22.1)

     
     
     により得られる行列 $V=\left[ \begin{array}{cccc}v_1 & v_2 & \cdots & v_n \end{array}\right]$が正則となるようにする．
  2. $K = - \Xi V^{-1}$を計算する．ただし $\Xi = \left[ \begin{array}{cccc} \xi_1 & \xi_2 & \cdots & \xi_n \end{array}\right]$である．

• $\Lambda$が複素数極 $\lambda_i = \alpha_i + j \beta_i$をもつ場合
  1. $\lambda_i$に共役な極を $\lambda_{i+1} = \alpha_i - j \beta_i$ととり
     $$\begin{eqnarray*} v_i &=& \{(A-\alpha_iI)^2 + \beta_i^2 I\}^{-1} \{(A-\alpha_iI)... ...I)^2+\beta_i^2I\}^{-1}\{\beta_iB\xi_i+(A-\alpha_iI) B\xi_{i+1}\} \end{eqnarray*}$$
     
     
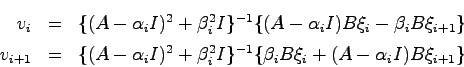
     により各$v_i$を求める．また，$\lambda_i$が実数極の場合には(22.1)式により$v_i$を求め，これらにより得られる $V=\left[ \begin{array}{cccc}v_1 & v_2 & \cdots & v_n \end{array}\right]$が正則となるようにする．
  2. $K = - \Xi V^{-1}$を計算する．

例6.4　システム

$$\dot{x} = \left[ \begin{array}{cc}1 & 1 0 & 1 \end{array}\right] x + \left[\begin{array}{c} 0 1 \end{array}\right]u$$

に対して極を $\sum = \{-1,-2\}$に設定する状態フィードバック則を求める． もとのシステムの極が$\{1,1\}$であり，$\sum$は単極のみからなるので， この$\sum$は制約条件を満たす．

1. $n=2,m=1$であるから，いま仮に$\xi_1=\xi_2=1$と置いてみる．すると
   
   $$v_1 = (A+I)^{-1}b = \frac{1}{4}\left[ \begin{array}{c}-1 ... ...= \frac{1}{9}\left[ \begin{array}{c}-1 3 \end{array}\right]$$
   
   
   であり，$V$は正則となる．
2. 
   
   $$K=-\left[ \begin{array}{cc}1 & 1 \end{array}\right] \cdot 36... ...ight]^{-1} = -\left[ \begin{array}{cc}6 & 5 \end{array}\right]$$
   
   
   となるから， $u=-\left[ \begin{array}{cc}6 & 5\end{array}\right]x+v$が求める状態フィードバック則である．

例6.5　例6.4と同じシステムに対して，極を $\sum=\{ -1 + j, -1-j\}$に設定する状態フィードバックを求める．

1. $\xi_1=\xi_2=1$と置くと，
   
   $$v_1 = \frac{1}{25}\left[ \begin{array}{cc}1 & 5 \end{array}\... ...frac{1}{25}\left[\begin{array}{cc}-7 & 15 \end{array}\right]^T$$
   
   
   となる．
2. $K=-\left[ \begin{array}{cc}5 & 4 \end{array}\right]$.

よって， $u=-\left[ \begin{array}{cc}5 & 4 \end{array}\right]x + v$が求める状態フィードバック則である．