


: 可制御性
: sysconh16
: 遷移行列の算出
古典制御理論では,例えば力学系の場合,運動方程式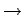 ラプラス変換
ラプラス変換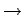 システムの伝達関数という流れでシステムの特性を考察した.これに対し,現代制御理論では,運動方程式
システムの伝達関数という流れでシステムの特性を考察した.これに対し,現代制御理論では,運動方程式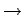 状態変数の導入
状態変数の導入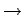 状態方程式という流れでシステムの特性を考察している.
状態方程式という流れでシステムの特性を考察している.
ここでは,上記のような古典制御と現代制御の流れの整合性を取るため,スカラー系において,伝達関数表現と状態方程式表現との関係を述べる.
[状態方程式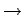 伝達関数] スカラ入力
伝達関数] スカラ入力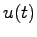 ,スカラ出力
,スカラ出力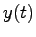 を持つ
線形システムの状態方程式表現
を持つ
線形システムの状態方程式表現
が与えられたとき,このシステムの伝達関数は次のようにして求められる.
ただし,状態変数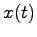 及び係数
及び係数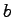 は
は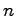 次ベクトル,係数
次ベクトル,係数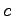 は
は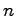 次横ベクトル
とする.(4.1),(4.2)式を,
次横ベクトル
とする.(4.1),(4.2)式を,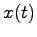 の初期条件を
の初期条件を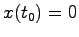 として
ラプラス変換すると
として
ラプラス変換すると
となる.したがって,(4.3)式より
となり,これを(4.4)式に代入すると
したがって,伝達関数
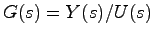 は
は
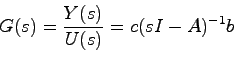 |
(4.5) |
となる.
例2.5 2次系
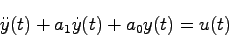 |
(4.6) |
を考える.ただし,系の初期状態は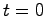 で
で
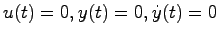 とする.このとき,状態変数を
とする.このとき,状態変数を
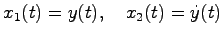 とすると,(4.5)式より
とすると,(4.5)式より
となる.したがって,状態方程式は
![\begin{displaymath}
\dot{x}(t) = \left[ \begin{array}{cc}0 & 1 -a_0 & -a_1 \e...
..., \quad
y = \left[ \begin{array}{cc} 1 & 0 \end{array}\right]x
\end{displaymath}](img173.png) |
(4.7) |
となる.さらに
と置けば,(4.7)式は簡単に
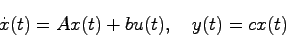 |
(4.8) |
となる.
上式(4.8)から伝達関数 を求めてみる.そのため,(4.8)式を
初期条件
を求めてみる.そのため,(4.8)式を
初期条件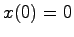 を考慮し,ラプラス変換すると
を考慮し,ラプラス変換すると
したがって,
となるから,
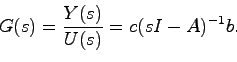 |
(4.9) |
(4.9)式を具体的に求めると,
となり,これと(4.9)式より
![\begin{displaymath}
G(s) = \frac{1}{s^2 + a_1s + a_0} \left[ \begin{array}{cc} 1...
...ray}{c} 0 1 \end{array}\right]
= \frac{1}{s^2 + a_1s + a_0}
\end{displaymath}](img181.png) |
(4.10) |
となる.
次に(4.6)式より直接伝達関数 を求めてみる.そのため(4.6)
式を初期条件のもとラプラス変換すると,
を求めてみる.そのため(4.6)
式を初期条件のもとラプラス変換すると,
となり,これから
が得られ,(4.10)式と同じになることがわかる.
例2.6 次の状態方程式で与えられるシステムを考える:
![\begin{displaymath}
\dot{x}(t) = \left[ \begin{array}{ccc}0 & 1 & 0 -a_0 & -a...
... = \left[ \begin{array}{ccc}1 & 0 & 0 \end{array}\right] x(t).
\end{displaymath}](img184.png) |
(4.11) |
ただし,初期条件は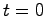 で
で
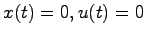 とする.
とする.
より,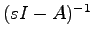 は
は
となる.よって,
となる.すなわち,この例で得られた伝達関数 は例2.5の伝達関数と同じ
ものになる.このことは,伝達関数表現では例2.5と例2.6を区別できないことになり,
状態方程式表現の方がシステムの多様性を表現できることを示している.
は例2.5の伝達関数と同じ
ものになる.このことは,伝達関数表現では例2.5と例2.6を区別できないことになり,
状態方程式表現の方がシステムの多様性を表現できることを示している.
例2.7 次の状態方程式で表されるシステムを考える.
(4.12),(4.13)式から伝達関数を求めれば
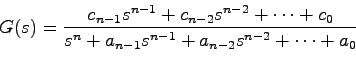 |
(4.14) |
が得られる.すなわち,(4.12),(4.13)式は古典制御理論における
一般的な伝達関数の状態方程式の一つを与えていることがわかる.



: 可制御性
: sysconh16
: 遷移行列の算出
endo
平成16年6月30日
![]() 伝達関数] スカラ入力
伝達関数] スカラ入力![]() ,スカラ出力
,スカラ出力![]() を持つ
線形システムの状態方程式表現
を持つ
線形システムの状態方程式表現
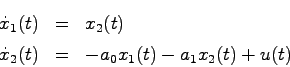
![\begin{displaymath}
A = \left[ \begin{array}{cc}0 & 1 -a_0 & -a_1 \end{array}...
...t],\quad
c = \left[ \begin{array}{cc} 1 & 0 \end{array}\right]
\end{displaymath}](img174.png)
![]() を求めてみる.そのため,(4.8)式を
初期条件
を求めてみる.そのため,(4.8)式を
初期条件![]() を考慮し,ラプラス変換すると
を考慮し,ラプラス変換すると
![\begin{displaymath}
(sI-A)^{-1} = \left[ \begin{array}{cc} s & -1 a_0 & s + a...
...t[ \begin{array}{cc}
s+a_1 & 1 -a_0 & s \end{array} \right]
\end{displaymath}](img180.png)
![]() を求めてみる.そのため(4.6)
式を初期条件のもとラプラス変換すると,
を求めてみる.そのため(4.6)
式を初期条件のもとラプラス変換すると,
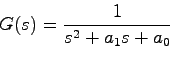
![\begin{displaymath}
(sI-A) = \left[ \begin{array}{ccc}
s & -1 & 0 a_0 & s + a_1 & 0 -1 & 0 & s-1 \end{array}\right]
\end{displaymath}](img186.png)
![\begin{displaymath}
(sI-A)^{-1} = \frac{1}{(s^2+a_1s + a_0)(s-1)}
\left[ \begin{...
...(s-1) & 0 \\
s+a_1 & 1 & s^2 + a_1s + a_0
\end{array}\right]
\end{displaymath}](img187.png)
![\begin{eqnarray*}
G(s) &=& c(sI-A)^{-1}b \\
&=& \frac{1}{(s^2+a_1s + a_0)(s-1)}...
... 0 1 2 \end{array}\right] \\
&=& \frac{1}{s^2+a_1s + a_0}
\end{eqnarray*}](img188.png)