


: この文書について...
: sysconh16
: 線形関数オブザーバ
システム
において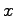 が直接観測できる場合には,図7.1(a)のように状態フィードバック則
が直接観測できる場合には,図7.1(a)のように状態フィードバック則
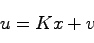 |
(27.1) |
によって閉ループ系の極を任意に配置できることを示した.しかし
によって与えられる出力しか観測できない場合には,この制御則は使えない.これに対処する方法として,前節で説明したように制御則(27.1)の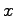 の代わりに,状態オブザーバによる状態の推定値
の代わりに,状態オブザーバによる状態の推定値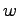 を用いて
を用いて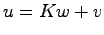 とすることが考えられる.これによって図7.1(b)のような出力フィードバック制御系が構成できる.本節ではこの制御系の極と,もとの状態フィードバック系,およびオブザーバの極との関係を調べる.
とすることが考えられる.これによって図7.1(b)のような出力フィードバック制御系が構成できる.本節ではこの制御系の極と,もとの状態フィードバック系,およびオブザーバの極との関係を調べる.
この出力フィードバック系を一つの線形システムみなして状態方程式を求めると
より
であるから
となる.ここで推定誤差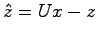 を用いて状態変数を
を用いて状態変数を
![$[ \begin{array}{cc}
x^T & z^T \end{array}]^T$](img1153.png) から
から
![$[ \begin{array}{cc}x^T & \hat{z}^T \end{array}]^T$](img1154.png) に変更する.
このとき
に変更する.
このとき
であるから
で変数変換すると
となる.ここで(8.6),(8.7),(8.8)式を用いて簡単化した.この式より以下のことがわかる.
- オブザーバを用いて実現した出力フィードバック系の伝達関数行列
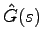 は
は
となり,状態が直接観測できるものとして設計した状態フィードバック系の伝達関数行列に等しくなる.
(注)上の式変形で
を用いた.
- オブザーバを用いて実現した出力フィードバック系の閉ループ極は
であるから,状態フィードバック系の極(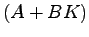 の固有値)とオブザーバの極(
の固有値)とオブザーバの極(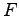 の固有値)との和よりなる.さらに,可制御可観測なシステムの場合には,これらの極を任意に設定できる.
の固有値)との和よりなる.さらに,可制御可観測なシステムの場合には,これらの極を任意に設定できる.
極の具体的な配置については,複素平面上で,オブザーバの極が,状態フィードバックの極よりもずっと左側にくるようにするのが望ましい.なぜならこのようにすることによって状態推定誤差をシステムの応答よりも速く0に収束させることができるからである.
例7.4 システム
に対して,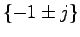 を極に配置する状態フィードバック則は,例6.5で求めたように
を極に配置する状態フィードバック則は,例6.5で求めたように
![$u=-[\begin{array}{cc}5 & 4\end{array}]x+v$](img1162.png) で与えられる.また,その極が
で与えられる.また,その極が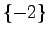 となるような状態オブザーバの一つは,例7.2で求めたように
となるような状態オブザーバの一つは,例7.2で求めたように
であたえられる.これらの結果を組み合わせて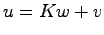 とすると,出力
とすると,出力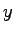 を用いた
出力フィードバック則
を用いた
出力フィードバック則
が得られる.これらより
と計算できるから,この制御側を用いた閉ループ系の状態方程式は
となる.計算すれば極は
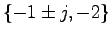 であることがわかる.
であることがわかる.



: この文書について...
: sysconh16
: 線形関数オブザーバ
endo
平成16年6月30日
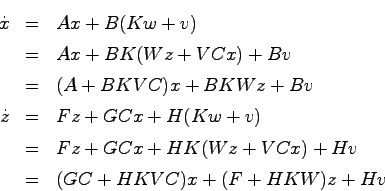
![\begin{displaymath}
\left[ \begin{array}{cc}
I_n & 0 U & -I_p \end{array}\right]
\left[ \begin{array}{c}x z \end{array}\right]
\end{displaymath}](img1155.png)
![\begin{displaymath}
T = \left[ \begin{array}{cc}I_n & 0 U & -I_p \end{array}\...
...\left[ \begin{array}{cc}I_n & 0 U & -I_p \end{array}\right]
\end{displaymath}](img1156.png)
![\begin{displaymath}
\bar{A} = T\tilde{A}T^{-1} = \left[ \begin{array}{cc}
A+BK &...
...de{C}T^{-1} = \left[ \begin{array}{cc}C & 0 \end{array}\right]
\end{displaymath}](img1157.png)
![\begin{eqnarray*}
\hat{G} &=& \bar{C}(sI-\bar{A})^{-1}\bar{B} \\
&=& \left[ \be...
...n{array}{c}B 0 \end{array}\right] \\
&=& C[(sI_n-A-BK)^{-1}B
\end{eqnarray*}](img1159.png)
![\begin{displaymath}
\left[ \begin{array}{cc} A_{11} & A_{12} 0 & A_{22} \end{...
...}^{-1}A_{12}A_{22}^{-1} \\
0 & A_{22}^{-1} \end{array}\right]
\end{displaymath}](img596.png)
![\begin{displaymath}
\det(sI-\bar{A}) = \det \left[ \begin{array}{cc}
sI_n-(A+BK)...
... & sI_p - F \end{array}\right]
= \det(sI_n-(A+BK))\det(sI_p-F)
\end{displaymath}](img1160.png)
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}1 & 1 0 & 1 \end{array}...
...]u,\quad
y = \left[ \begin{array}{cc}1 & 1\end{array}\right] x
\end{displaymath}](img1039.png)
![\begin{eqnarray*}
\dot{z} &=& -2z-9y-2u \\
w &=& \left[ \begin{array}{c}-1 1...
...}\right]z + \left[ \begin{array}{c}-2 3 \end{array}\right] y
\end{eqnarray*}](img1088.png)
![\begin{displaymath}
A+BKVC = \left[ \begin{array}{cc}1 & 1 -2 & -1 \end{array...
... \begin{array}{cc}-5 & -5 \end{array}\right], \quad
F+HKW = -4
\end{displaymath}](img1164.png)
![\begin{displaymath}
\left[ \begin{array}{c}
\dot{x} \dot{z} \end{array}\right...
...left[ \begin{array}{c}0 -1 \hline -2 \end{array}\right]v
\end{displaymath}](img1165.png)