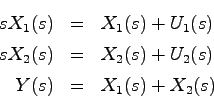: 同値変換
: sysconh16
: 可制御性
本節では,与えられたシステムに対し,適当な有限時刻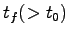 までの零入力によりシステムの初期状態を知ることができるか(可観測性)について考察する.
までの零入力によりシステムの初期状態を知ることができるか(可観測性)について考察する.
まず,可観測性の定義を述べる.
[可観測性] ある有限の時刻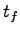 までの零入力応答
までの零入力応答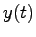 を観測することによって,初期状態
を観測することによって,初期状態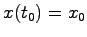 を一意に決定できるとき,システムは可観測であるという.
を一意に決定できるとき,システムは可観測であるという.
可観測性の判定条件にも可制御性と同様,いくつかの条件があるが,最も一般的なものとしては,次の可観測行列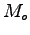 を利用したものが挙げられる.
を利用したものが挙げられる.
定理 (可観測性の判定規範)次の状態方程式で与えられるシステムを考える.
ただし,係数行列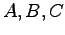 はそれぞれ
はそれぞれ
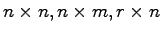 の定数行列とする.
の定数行列とする.
このとき,システム(20.1),(20.2)が可観測であるための必要十分条件は
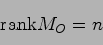 |
(6.3) |
が成り立つことである.ここで,可観測性行列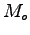 は以下の式で定義される
は以下の式で定義される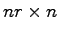 定数行列である:
定数行列である:
![\begin{displaymath}
M_O = \left[ \begin{array}{c}C CA \vdots CA^{n-1} \end{array} \right]
\end{displaymath}](img277.png) |
(6.4) |
例3.4 次のシステムを考える.
このシステムに対する可観測性行列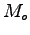 は
は
であるから
となり,システムは可観測である.
次に,(実際にはあまり有効ではないが)このシステムのブロック線図を求め、状態と出力との関係を
視覚的に捉えてみる。このため(21.1),(21.2)式を
ラプラス変換すると
となり,図3.6のようにブロック線図が得られる.図3.6より,出力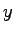 はすべての状態
はすべての状態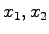 に依存している.このことはシステムが可観測であることを示している.
に依存している.このことはシステムが可観測であることを示している.
例3.5 システム
を考える.このシステムの可観測性行列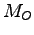 は
は
より,
となり,システムは可観測でない.
上の例題と同様,このシステムのブロック線図を求める。(21.4),(21.5)を
ラプラス変換すると
となり,図3.7のブロック線図が得られる.図3.7では,出力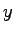 はすべての状態
はすべての状態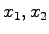 に依存しているが,可観測性行列
に依存しているが,可観測性行列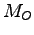 によると,このシステムは可観測ではない.
これは例3.3と同様,適当な状態変数を選ぶことで,出力に影響を与えない状態を作ることができることを示している.このようにブロック線図による表現では、前項の可制御性同様、可観測性の判別には十分でないことが
わかる。
によると,このシステムは可観測ではない.
これは例3.3と同様,適当な状態変数を選ぶことで,出力に影響を与えない状態を作ることができることを示している.このようにブロック線図による表現では、前項の可制御性同様、可観測性の判別には十分でないことが
わかる。



: 同値変換
: sysconh16
: 可制御性
endo
平成16年6月30日
![]() までの零入力応答
までの零入力応答![]() を観測することによって,初期状態
を観測することによって,初期状態![]() を一意に決定できるとき,システムは可観測であるという.
を一意に決定できるとき,システムは可観測であるという.
![]() を利用したものが挙げられる.
を利用したものが挙げられる.
![\begin{displaymath}
M_O = \left[ \begin{array}{cc}1 & 1 0 & -1 \end{array}\right]
\end{displaymath}](img281.png)
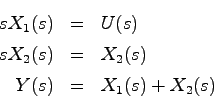
![\begin{displaymath}
M_O = \left[ \begin{array}{cc} 1 & 1 -1 & -1 \end{array} \right]
\end{displaymath}](img287.png)