ファジィ推論(1)

　ファジィ制御で最も多く応用されているのが、この直接法によるファジィ推論です。その推理手順では、まず前提条件として条件命題と事実を用意します。そして、そこから帰納的に結論を導き出します。例えば、以下に示す形態です。

条件命題：

パソコンが

高ければ、

パソコンの

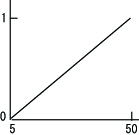性能は良い

事実　　　 ： パソコンは高い。

結論　　　 ： パソコンの性能は良い。

ここで条件命題、事実、結論における「高い」、「性能は良い」はファジィ集合で与えられています（パソコンの性能は0〜100までの数値で評価されるものとします）。そのため、直接法では「パソコンは少し高い」という事実が与えられれば、「パソコンの性能は少し良い」という結論（60という評価）を得られることになります。また、条件命題が複数になれば結論もそれだけ導かれることになります。その場合は、全ての結論を合成した結果を最終的な結論とします。例えば、

条件命題：

パソコンが

新しければ、

パソコンの

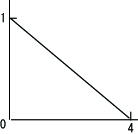性能は良い

事実　　　 ： パソコンは古い。