ファジィ推論(3)

　マムダニのファジィ推論ではまず前件部の適合度（事実が前件部をどの程度満たしているかという度合い）を求めます。例えば以下に示す条件命題が与えられたとします。

条件命題：

パソコンが

高ければ、

パソコンの

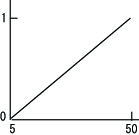性能は良い

　
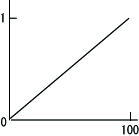　この時、得られる結論は前件部の適合度によって変化するものです。（「パソコンは高い」という事実が与えられれば、「パソコンの性能は良い」という結論が得られ、「パソコンは安い」という事実が与えられれば、「パソコンの性能は悪い」という結論が得られます。）条件命題にはファジィ集合が用いられています。ファジィ集合は メンバシップ関数によって定義されていますが、前件部のそれはパソコンの値段によって0〜1のメンバシップグレード を与えるものです。例えば、5万円以下のパソコンを0、50万円以上のパソコンを1、それ以外は値段に応じて度合いをつけるメンバシップ関数だったとします。その場合、事実としてパソコンの値段は25万円であると入力されたら、メンバシップグレードは0.5となります。これが前件部の適合度となるわけです。あとは適合度に応じて 後件部のファジィ集合から結論を導いてやればいいわけです。それでは、次のような条件命題が与えられた場合、適合度はどうなるのでしょうか？

条件命題：

パソコンが

高くて

新しければ、

パソコンの

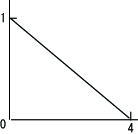性能は良い

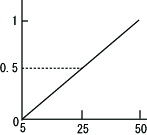
　この場合は、「高い」と「新しい」でそれぞれ適合度を求めて低い方を前件部の適合度とします。例えば、「パソコンの値段は25万円で3年前のものである」という事実が与えられれば、「新しい」に関する適合度の方が低くなるので、そちらを前件部の適合度とします（条件が増えた場合も同じ手法で適合度を決定します）。

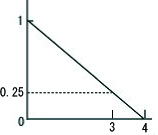「高い」の適合度が0.5であり、「新しい」の適合度が0.25であるため、全体の適合度は0.25となる。

戻る 次へ