3.2 カオスニューロンモデル

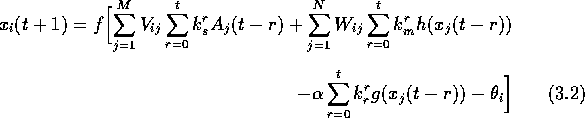
カオスニューロンモデルを定式化するに当たって、次のことを考慮する。

• 相互結合ネットワークのような、他のニューロンからのフィードバック入力
• 階層型ネットワークのような、そのニューラルネットワーク外部からの入力

上記のネットワークは次章で詳しく述べることとし、フィードバック入力と外部入力を考慮してカオスニューロンのダイナミクスは次のように表せる。

 

ここで、各変数並びに定数は ：時刻 (t+1) でのニューロン i の出力値。出力は０から１の間の数値であり、また時間は離散的に刻まれる。出力関数はシグモイド関数（図3.3）を用いる。

：時刻 t のニューロン j の出力に対するニューロン i へのフィードバック入力。

N ：ニューロンのフィードバック入力線の総数。

M ：ニューロンの外部入力線の総数。

：外部入力 A(t) からニューロン i へのシナプス結合の強さ。

：ニューロン i からニューロン j へのシナプス結合の強さ。

：外部入力に関する記憶の減衰定数 。

：相互結合入力に関する記憶の減衰定数 。

：不応性に関する減衰定数 。

g ：ニューロンの出力と不応性の大きさとの関係を与える関数。

：ニューロンの閾値。

：定数パラメータ

  
図 3.3: シグモイド関数

  
図 3.4: カオスニューロンモデル

また、ニューロン i の内部状態を、

   

と定義する。関数 g と h を恒等関数として扱えば式(3.4)〜式(3.5)は式(3.7)〜式(3.8)のように単純化できる。

   

ただし

 

とする。最終的なカオスニューロンの出力は次のようになる。

 

となる。ここで は、シグモイド関数（図3.3）である。