5.2 一般化デルタルール

  本節では、多くの学習法の中からラメルハートらが提案した バックプロパゲーション(1987)について説明する前に、 その考えの元になる一般化デルタルールについて説明することにする。 ニューラルネットワークに学習させる際にある値を入力した場合、 その時の出力が理想の出力とどれだけ異なっているかを示し、 学習の評価をするものとして、次のような``誤差関数 E'' を考える。

 

: ある入力パターン c に対して出力素子 j が出すべき望ましい出力。

: 出力素子 j の実際の出力。

このような形の誤差関数を最小にする手続きを一般に``最小2乗誤差'' (least mean square, LMS)法という。 はその時の素子間の結合の重み で決まるため、 誤差関数も重みに関して陰に定義された関数となる。 したがって、各重みの値を軸としてできる空間を考えれば、 E は重み空間上の超曲面として``誤差曲面"を与えることになる。 任意の重み状態から、この誤差曲面の極小値に達するには、例えば各重みを に比例した量

 

ずつ変化させていけばよいことになる。これは、誤差曲面上を、 最も急な傾斜方向に進んでいくことに相当し、このような学習則を一般に 最急降下法(gradient decent method)という。

さて、ある素子 j は他の素子 i の出力 を入力として受け、 結合荷重 を乗じて加えたものを入力の総和とする。

 

そして、出力 は入力の総和に単調増加関数 f を施したもので 表わされることにする。

 

ただし、しきい値は結合荷重の1つとして含まれていると考える。 また、 関数 f はシグモイド関数(式(3.4))を用いることにする。

このように素子の性質を定義されているとすれば、 式(5.2)は合成関数の微分公式により

 

と展開できる（添字 c は省略した）。 式(5.3)(5.4)を微分して代入すれば、

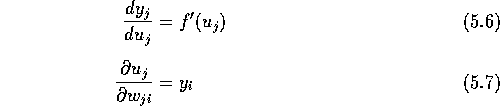
であるので、結局式(5.2)は

 

となる。中間層が学習しない場合、 の項は 式(5.1)を微分することにより簡単に

と求めることができるので、式(5.8)より

という学習則が得られる。これを、一般化デルタルールと呼ぶ。 例えば f が式(3.4)で与えられる場合

 

より

という形になる。 式(5.11)の方法では、すべての入出力パターンが与えられた後に はじめて結合荷重を変化させることになるが、 が十分に小さければ、 パーセプトロンのように各入出力が与えられるごとに結合荷重を反復的に変化させる。 すなわち

としても、全体の変化量は最急降下法とほぼ等しくなる [5]。