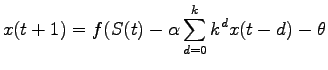カオスニューロンモデル

合原らによるヤリイカの巨大軸索を用いた電気生理実験により、神経膜が周期的電流刺激に対してカオス応答を有することを明らかにされた。しかしながら、式(2.1)〜式(2.3)のモデルの応答はほとんどが絶対安定点にたどり着くか周期解となり、カオスを生成しない。これは、式(2.1)〜式(2.3)で考慮しなかった実際のニューロンの何らかの特性が、カオスの生成に寄与しているためであると考えられる。

この何らかの特性としては不応性が挙げられる。不応性とは前にも記したように、神経細胞が興奮した直後は次の活動電位が生成されにくくなることである。これまではニューロンの活動電位生成過程が全か無かの法則に従うことは常識であり、これまではそれに基づいてモデルが作成されてきた。しかし合原らによると、空間固定の条件で注意深い実験を行うと、実際の神経膜の活動電位生成過程は、厳密には全か無の法則には従わず、急嵯ではあるが連続的に応答の大きさが変化することが分かった。この不成立ゆえにニューロンにカオスが生成されるのである。

これら2点の特性・性質を再現できる神経細胞のモデルをカオスニューロンモデルと呼び、式(3.2)で表す。

$$x(t+1) = f(S(t)-\alpha\sum_{d=0}^{k}{k^dx(t-d)-\theta}$$ (6)

$x(t)$は時刻$t$における出力、$S(t)$は時刻$t$における入力、$\alpha$は不応性の項に対する係数、$k$は不応性の時間減衰定数、$\theta$は閾値をそれぞれ表す。ここで関数$f(y)$は式(2.4)で定義されるシグモイド関数であり、$\epsilon$はこの関数の傾きの急嵯を表す定数である。

また、入力$S(t)$を時刻$t$によらず一定とし、

$$a = (S(t)-\theta)(1-k)$$ (7)

とおくと、式(3.2)は次の式(3.4)に変形される。

$$\begin{array}{l} x(t+1) = f(y(t+1)) y(t+1) = ky(t)-\alpha x(t)+a \end{array}$$ (8)