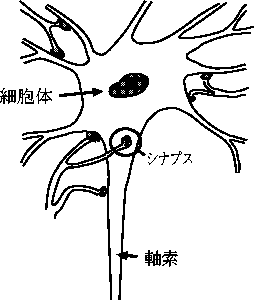
図 2.1: 神経細胞の構造
ニューロン(neuron)とは、人間および動物の神経細胞のことを指す。 ニューロンは人間1人の脳におよそ100億から1000億もの数があるとされている。 神経細胞の概略図を図 6.5 に示す。
これらニューロンは本体と言える細胞体、そこから多様に枝分かれした樹状突起、 そして細胞体から1本だけ出ている軸索、 の3つによって構成されている。 軸索は末端で複数に枝分かれしており、 それを用いて他の神経細胞の細胞体や樹状突起と結合し、 ネットワークを形成している。 この結合をシナプス結合と呼ぶ。 1つの神経細胞が受けるシナプス結合の数は、数百ないし数千、 時には数万に及ぶことになる。
これを模したものが、 ニューラルネットワーク研究並びに本研究で用いられるニューロンである。
1943年にマッカロ(W.S.McCulloch)とピッツ(W.Pitts)によって提案され、 後の研究者により多少修正が加えられた、ニューロンの基本的性質を以下に示す。 ニューロンの動作はまず、 他のニューロンから出力された信号を受けとることから始まる。 ニューロンとニューロンとの間の結合の強さは それぞれのニューロンで異なるとされており、 ニューロンからニューロンへの信号はその結合の強さに応じたものが伝えられる。 その信号がある程度の強さを持つと、ニューロンは突然パルス信号を出力する。 これはニューロンの「発火」もしくは「興奮」と呼ばれる現象である。 ここで出力された信号が他のニューロンの信号となり、 これの繰り返しによりネットワークを形成する。 以上がニューロンの最も基本的な性質である。 図 6.5 にニューロンのモデルを示す。
この図の ![]() は対象のニューロンの入力のi番目の結合からの入力であり、
は対象のニューロンの入力のi番目の結合からの入力であり、
![]() はその入力と対象ニューロンとのシナプス結合の強さを表す。
はその入力と対象ニューロンとのシナプス結合の強さを表す。
![]() はこのニューロンが持つしきい値であり、
ニューロンへと伝わる信号がこれを越えると、興奮状態となる。
yはこのニューロンの出力である。
また、このモデルはニューロンの基本的性質を
情報処理のモデルとして置き換えたものであり、
それぞれの値は物理的な単位を持たない。
以上のことを表すと下の式になる。
はこのニューロンが持つしきい値であり、
ニューロンへと伝わる信号がこれを越えると、興奮状態となる。
yはこのニューロンの出力である。
また、このモデルはニューロンの基本的性質を
情報処理のモデルとして置き換えたものであり、
それぞれの値は物理的な単位を持たない。
以上のことを表すと下の式になる。
式(2.5) において、 ![]() はi番目の入力信号を示し、
はi番目の入力信号を示し、
![]() はその入力と対象のニューロンとの結合の強さ、また
はその入力と対象のニューロンとの結合の強さ、また ![]() はしきい値を示す。
はしきい値を示す。
![]() の範囲は正負にまたがり、それぞれ興奮性結合、抑制性結合を表している。
uはニューロンの内部状態と呼ばれ、またこの式は
の範囲は正負にまたがり、それぞれ興奮性結合、抑制性結合を表している。
uはニューロンの内部状態と呼ばれ、またこの式は
と表すことができるため、しきい値 ![]() とは、
常に1を出力するニューロンから重み
とは、
常に1を出力するニューロンから重み ![]() で結合していることと
同義であると見なすことができる。
で結合していることと
同義であると見なすことができる。
f(u)は出力関数である。
出力関数f(u)には数多くのものが考えられるが、 基本的なものとしては0または1を出力するステップ関数である。
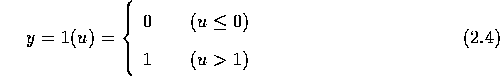
こういった出力特性を持ったニューロンモデルを、パーセプトロンと呼ぶ。 パーセプトロンは、ニューラルコンピュータの原点であると同時に、 現在でも基本要素として重要なものである。 これは、ローゼンブラットによって提案された(Rosenblatt,1961) パターン認識(認識:perception)機械としてのニューラルネットワークであり、 名前もそこからつけられている。 その取り上げ方や応用はさまざまなものが可能であり、 例えば学習能力を持つ2値論理関数要素と見ることもできるし、 実時間信号を処理する適応フィルタと見ることもできる。 パーセプトロンは、入力ベクトルが各結合加重を各軸とする 超空間中の超平面のどちらにあるかを1か0で出力でき、 線形分離可能な識別であればこの超平面を学習できることが証明されている。 また、線形分離不可能であっても中間(連合)層で前処理を行なって 線形分離可能にすることによってどのような識別でもできるようになる。 しかし、この前処理が最も難しい問題であり、 必要となる前処理がわかっているような問題は わざわざ線形分離するための学習をする必要のないものが多い。 パーセプトロンは発表当時の期待とは裏腹に、 どのような分類にも対応できるように連合層の素子を用意するとなると、 その数は天文学的な数字になる等といった否定的な結論が ミンスキー(Minsky)により証明され、 ニューラルネットワークの研究熱は冷めていった。[3]
現在、一般的に使用されている出力関数f(u)は シグモイド関数と呼ばれるものである。 以下にその一例を示す。
この関数の出力特性は図 6.5 のように
![]() の連続した値である。
実際の脳の神経細胞の出力にはばらつきがあるため、
0か1のステップ関数を用いるよりは、
このシグモイド関数の方が
よりニューロンの出力関数にふさわしいものと言える。
の連続した値である。
実際の脳の神経細胞の出力にはばらつきがあるため、
0か1のステップ関数を用いるよりは、
このシグモイド関数の方が
よりニューロンの出力関数にふさわしいものと言える。