


: 状態フィードバックによる極配置問題
: sysconh16
: 線形システムに対するリアプノフの安定定理
前節の定理5.6では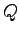 を正定ととったが,可観測性に関連するある条件を満たせば
を正定ととったが,可観測性に関連するある条件を満たせば
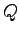 は準正定であってもよいことが知られている.本節ではこれについて説明する.
は準正定であってもよいことが知られている.本節ではこれについて説明する.
定理5.7 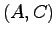 を可観測対とする.このとき
を可観測対とする.このとき が漸近安定行列(すなわち
が漸近安定行列(すなわち
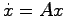 が漸近安定)であるための必要十分条件は
が漸近安定)であるための必要十分条件は
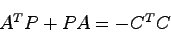 |
(19.1) |
の解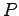 が正定となることである.
が正定となることである.
証明 十分性を示す.リアプノフ関数の候補として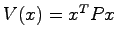 ととる.明らかに
ととる.明らかに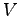 は正定であり,
は正定であり,
より
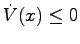 であるから
であるから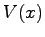 はリアプノフ関数である.この
はリアプノフ関数である.この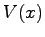 が定理5.5の条件2'.を満たすこと,すなわち任意の
が定理5.5の条件2'.を満たすこと,すなわち任意の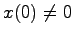 に対するシステム(17.1)の解
に対するシステム(17.1)の解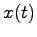 が
が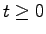 において恒等的には
において恒等的には
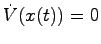 とはならないことを示す.
とはならないことを示す.
背理法により証明するため任意の初期値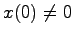 に対する
に対する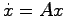 の解
の解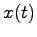 が恒等的に
が恒等的に
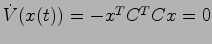 を満たすものとする.すると
を満たすものとする.すると
が得られ,これを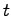 に関して
に関して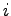 回微分すると
回微分すると
となり,これらをまとめると
![\begin{displaymath}
\left[ \begin{array}{c}
C CA \vdots CA^{n-1} \end{array}\right] e^{At}x(0) = 0
\end{displaymath}](img893.png) |
(19.2) |
となる.ところが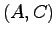 は可観測対であり,
は可観測対であり,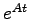 は正則行列であるので
は正則行列であるので
である.これと(19.2)式より明らかに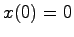 でなければならず,矛盾する.
したがって
でなければならず,矛盾する.
したがって
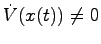 となり,原点は漸近安定である.
となり,原点は漸近安定である.
必要性については省略する(各自で確認).
endo
平成16年6月30日
![]() を可観測対とする.このとき
を可観測対とする.このとき![]() が漸近安定行列(すなわち
が漸近安定行列(すなわち
![]() が漸近安定)であるための必要十分条件は
が漸近安定)であるための必要十分条件は
![]() ととる.明らかに
ととる.明らかに![]() は正定であり,
は正定であり,
![]() に対する
に対する![]() の解
の解![]() が恒等的に
が恒等的に
![]() を満たすものとする.すると
を満たすものとする.すると
![\begin{displaymath}
{\rm rank}\left[ \begin{array}{c}C CA \vdots CA^{n-1}\end{array}\right]
e^{At} = n
\end{displaymath}](img894.png)