


: 同一次元状態オブザーバ
: sysconh16
: 状態フィードバックによる多入力システムの極配置
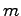 入力
入力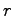 出力で,
出力で,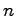 次元状態変数をもつ線形システム
次元状態変数をもつ線形システム
において,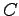 が
が
を満たすとする.明らかに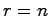 の場合には,
の場合には,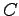 が正則となるので,状態
が正則となるので,状態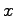 は
は
により直接知ることができる.しかし一般には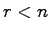 であり,この場合は
であり,この場合は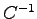 が存在せず,ある時刻
が存在せず,ある時刻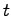 における状態
における状態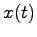 を知りたいと思えば,その時刻までの観測可能な出力
を知りたいと思えば,その時刻までの観測可能な出力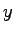 ,および制御装置で定める入力
,および制御装置で定める入力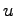 の値から
の値から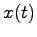 の値を推定する必要がある.
そこで,システム(8.1),(8.2)に対して,
の値を推定する必要がある.
そこで,システム(8.1),(8.2)に対して,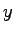 と
と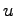 を入力とする新たなシステム
を入力とする新たなシステム
を考える.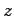 及び
及び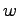 は,この新たなシステムの
は,この新たなシステムの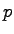 次元状態ベクトル及び
次元状態ベクトル及び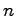 次元出力ベクトルである.
この出力
次元出力ベクトルである.
この出力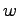 が
が
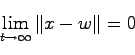 |
(23.3) |
を満足するとき,(23.3),(23.3)は,システム(23.1),(23.2)に対する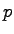 次元状態オブザーバであるという.このとき次の定理が導ける.
次元状態オブザーバであるという.このとき次の定理が導ける.
定理 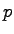 次元システム(23.3),(23.3)は,その係数行列
次元システム(23.3),(23.3)は,その係数行列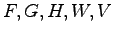 が次の条件を満たすとき,システム(23.1),(23.2)に対する状態オブザーバである.
が次の条件を満たすとき,システム(23.1),(23.2)に対する状態オブザーバである.
- 適当な
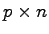 行列
行列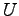 を選んだとき,次の3つの式を満足する.
を選んだとき,次の3つの式を満足する.
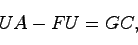 |
(23.4) |
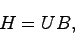 |
(23.5) |
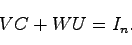 |
(23.6) |
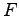 は安定行列(固有値の実部がすべて負である行列)である.
は安定行列(固有値の実部がすべて負である行列)である.
証明 (8.1),(8.2),(8.3)より
を得る.上式右辺に(8.6),(8.7)を用いると
となる.したがって
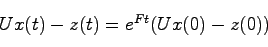 |
(23.7) |
を得る.他方,(8.2),(8.4),(8.8)より
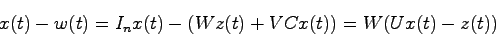 |
(23.8) |
となる.(8.9),(8.10)と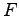 が安定行列であることから
が安定行列であることから
が成り立ち,(8.5)式を満たす.
以上の証明から判るように,オブザーバの状態変数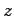 は,もとのシステムの状態変数
は,もとのシステムの状態変数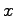 の線形関数
の線形関数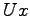 の推定値と考えることができる.そうなるための条件が(8.6)及び(8.7)である.また,その推定誤差
の推定値と考えることができる.そうなるための条件が(8.6)及び(8.7)である.また,その推定誤差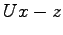 が,
が,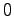 に収束する条件が条件2.である.さらに
に収束する条件が条件2.である.さらに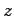 と
と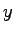 から構成される
から構成される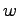 が,
が,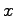 の推定値となるための条件が(8.8)式である.
の推定値となるための条件が(8.8)式である.



: 同一次元状態オブザーバ
: sysconh16
: 状態フィードバックによる多入力システムの極配置
endo
平成16年6月30日
![]() 入力
入力![]() 出力で,
出力で,![]() 次元状態変数をもつ線形システム
次元状態変数をもつ線形システム
![]() 次元システム(23.3),(23.3)は,その係数行列
次元システム(23.3),(23.3)は,その係数行列![]() が次の条件を満たすとき,システム(23.1),(23.2)に対する状態オブザーバである.
が次の条件を満たすとき,システム(23.1),(23.2)に対する状態オブザーバである.
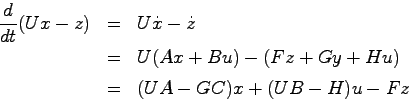
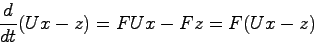
![]() は,もとのシステムの状態変数
は,もとのシステムの状態変数![]() の線形関数
の線形関数![]() の推定値と考えることができる.そうなるための条件が(8.6)及び(8.7)である.また,その推定誤差
の推定値と考えることができる.そうなるための条件が(8.6)及び(8.7)である.また,その推定誤差![]() が,
が,![]() に収束する条件が条件2.である.さらに
に収束する条件が条件2.である.さらに![]() と
と![]() から構成される
から構成される![]() が,
が,![]() の推定値となるための条件が(8.8)式である.
の推定値となるための条件が(8.8)式である.