


: 最小次元状態オブザーバ
: sysconh16
: 状態オブザーバの定義
本節では,状態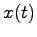 と同一の次元数をもつ状態オブザーバの一つを与える.
すなわち,
と同一の次元数をもつ状態オブザーバの一つを与える.
すなわち,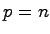 の場合を考える.
の場合を考える.
まずシステム(8.1),(8.2)のモデルを
とおき,推定誤差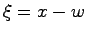 を考えると,
を考えると,
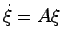 となる.したがって,
となる.したがって, が安定行列ならば
が安定行列ならば
であるから,システム(8.11),(8.12)は,一つの状態オブザーバとなっている.しかしその推定値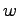 の真値
の真値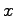 への収束速度は
への収束速度は に依存する.この収束速度を高め,また,安定でない
に依存する.この収束速度を高め,また,安定でない に対しても適用できるように,制御対象の出力
に対しても適用できるように,制御対象の出力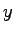 とそれに対応するモデルからの推定出力
とそれに対応するモデルからの推定出力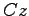 との偏差にフィードバックゲイン
との偏差にフィードバックゲイン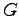 を乗じてモデルに加えて
を乗じてモデルに加えて
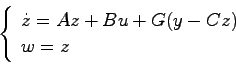 |
(24.3) |
とする.これは(8.3),(8.4)式において
と取ることに対応する.
したがって,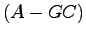 が安定行列となるように
が安定行列となるように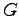 を選ぶことができれば,
を選ぶことができれば,
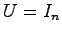 とすることにより定理7.1の条件を満たし,システム(8.13)が
(8.1),(8.2)に対する同一次元状態オブザーバとなる.
さらにオブザーバの極,すなわち行列
とすることにより定理7.1の条件を満たし,システム(8.13)が
(8.1),(8.2)に対する同一次元状態オブザーバとなる.
さらにオブザーバの極,すなわち行列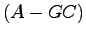 の固有値を任意に配置できれば,
推定誤差
の固有値を任意に配置できれば,
推定誤差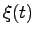 を任意の速さで0に収束させることができる.
これに関して次の定理が成り立つ.
を任意の速さで0に収束させることができる.
これに関して次の定理が成り立つ.
定理7.2 システム(8.1),(8.2)に対して,任意に設定した極をもつ同一次元状態オブザーバ(8.13)が存在するための必要十分条件は,対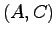 が可観測なことである.
が可観測なことである.
証明 対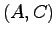 が可観測であることは,対
が可観測であることは,対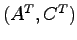 が可制御であることに等しく,したがって,定理6.2より
が可制御であることに等しく,したがって,定理6.2より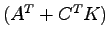 の固有値を任意に設定できることに等しい.
このことは
の固有値を任意に設定できることに等しい.
このことは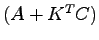 の固有値を任意に設定できることに等しく,これより(8.13)で
の固有値を任意に設定できることに等しく,これより(8.13)で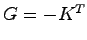 としたものが設定された極をもつ同一次元状態オブザーバとなる.
としたものが設定された極をもつ同一次元状態オブザーバとなる.
1出力システムについてはアッカーマンのアルゴリズムを適用できる.すなわち,設定したい極を
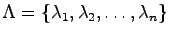 とし,
とし,
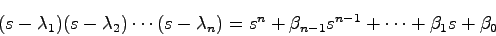 |
(24.4) |
とするとき,(21.7)式より,次式が得られる.
例7.1 システム
に対して,
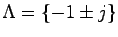 を極とする同一次元状態オブザーバを求める.
まずこのシステムは可観測であるから,このようなオブザーバは存在する.
そこで,(24.5)より,
を極とする同一次元状態オブザーバを求める.
まずこのシステムは可観測であるから,このようなオブザーバは存在する.
そこで,(24.5)より,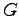 は
は
と求められる.
よって同一次元状態オブザーバは,(8.13)より
で与えられる.



: 最小次元状態オブザーバ
: sysconh16
: 状態オブザーバの定義
endo
平成16年6月30日
![]() と同一の次元数をもつ状態オブザーバの一つを与える.
すなわち,
と同一の次元数をもつ状態オブザーバの一つを与える.
すなわち,![]() の場合を考える.
の場合を考える.
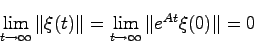
![]() が可観測なことである.
が可観測なことである.
![]() が可観測であることは,対
が可観測であることは,対![]() が可制御であることに等しく,したがって,定理6.2より
が可制御であることに等しく,したがって,定理6.2より![]() の固有値を任意に設定できることに等しい.
このことは
の固有値を任意に設定できることに等しい.
このことは![]() の固有値を任意に設定できることに等しく,これより(8.13)で
の固有値を任意に設定できることに等しく,これより(8.13)で![]() としたものが設定された極をもつ同一次元状態オブザーバとなる.
としたものが設定された極をもつ同一次元状態オブザーバとなる.
![]() とし,
とし,
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}1 & 1 0 & 1 \end{array}...
...]u,\quad
y = \left[ \begin{array}{cc}1 & 1\end{array}\right] x
\end{displaymath}](img1039.png)
![\begin{eqnarray*}
G &=& \left\{ \left[ \begin{array}{cc}
1 & 2 0 & 1 \end{arr...
...ght] \\
&=& \left[ \begin{array}{cc}-1 & 5 \end{array}\right]^T
\end{eqnarray*}](img1041.png)
![\begin{eqnarray*}
\dot{z} &=& \left[ \begin{array}{cc}2 & 2 -5 & -4 \end{arra...
... +
\left[\begin{array}{c} 0 1 \end{array}\right]u \\
w &=& z
\end{eqnarray*}](img1042.png)