SPIN-OUTs solution sequence follows the same pattern as that Chinese Ring Puzzle, a puzzle which may have been invented as early as 200 AD and has been popular for centuries.
For both puzzles, the solution involves a sequential movement, binary code pattern. Put simply, this means that each piece of the puzzle can be in only one of two positions at any given time. The world "binary" means two.
In SPIN-OUTs case, each disk starts in a vertical position in relation to the base. The object is to turn all disks horizontal, which will allow the slide to unlock and to come free. Because of the relationship between the disks, however, they can be turned only in a specific sequence.
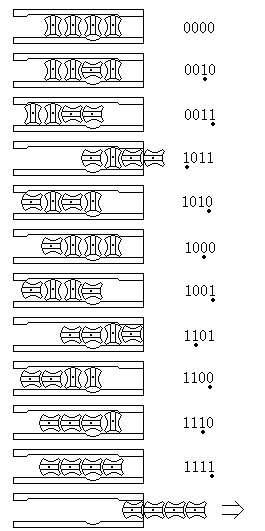
Figure 1 shows the solution pattern for a four disk SPIN-OUT puzzle. (A four disk SPIN-OUT is used for illustration purposes only, scene the solution is short enough to diagram here.) The figure shows both the disks as they really are, and as represented by the numbers "0" and "1". "0"'s are used for vertical disks, with "1"'s representing horizontal disks. The "*" indicates where the disks are to be turned on a given move.
Careful observers will note that there is a two part principle at work in the solution pattern.
1) Every second move switches the outermost disc from a "0" to a "1" and back again.
2) The remaining moves, those which do not switch the outermost disk, always switch the disk immediately to the left of the rightmost "0" (vertical) disk to its opposite position, "0" or "1".
Interestingly, SPIN-OUTs solution code sequence is exactly the same as the Gray binary code, a binary based counting system named after Frank Gray, a colleague of *Keister's at Bell Labs. Gray created this code in the 1930's to provide an error correcting technique for electronics communications. It is still used today as a basis for electronic switching and for computer logic.
(これは上の英文の和訳です。)
スピンアウトの解法の連続は、西暦 200 年ぐらいに発明され何世紀にも渡って親しまれてきた"Chinese Ring Puzzle" というパズルの解法と通じている。この両方のパズルの解法は 2 進数コードの一連の動きに関係している。簡潔にいえば、パズルのそれぞれのピースは、特定の時において2つのうちの1つの状態に対応しているのである。"binary"の世界は 2 を表している。
スピンアウトの場合、それぞれの円盤はすべて垂直になった状態から始まり、これは基本となる状態である。このパズルの目的は、すべての円盤を水平な状態にして、スライドを取り外し可能な状態にすることである。しかし、円盤同士の関係により、円盤は特定の向きにしか回転させることができない。
図 1 は 4 つの円盤のスピンアウトの模範解答である。(4 つの円盤のスピンアウトは、ここで図示するのに十分解法が短いので、説明図として使っている。) この図は円盤が、実際にどんな状態か、"0" と "1" によって表されているか、ということを示している。"0" は垂直な円盤で、"1" は水平な円盤を表している。"*" のマークはこの状態でどのディスクが回転されるかを示している。
賢明な諸君らは、解法のパターンがある 2 つの法則によって決まることに気付くだろう。
1) 2 手ごとに最も外側の円盤を "0" から "1" にしまた、元に戻す。
2) その他の外側の円盤の向きを変えない動きではいつも、一番右側にある "0" (垂直) の円盤の左隣にある円盤の向きを違う向き ("0" もしくは "1") に変える。
面白いことに、スピンアウトの解法の規則はまさにグレイの 2 進数コードと同じなのである。グレイの 2 進数コードは、ベル研究室で *ケイスター と同僚だったフランク グレイが名づけた計算システムを基本にした 2 進法である。グレイは 1930 年にこのコードを、電子工学の通信に対して誤りを訂正するための技術として創り出した。これは今日も電子工学の切り替え、コンピューターの論理の基本として使われている。
*Keister … SPIN-OUT を創った Willam Keister 氏のこと。
ちなみに、所先生の所持している SPIN-OUT の発売元は Binary Arts 社で、社長は Bill Ritchie 氏。
上の文章は SPIN-OUT の取扱説明書 (英語) から引用したものです。しかし、和訳は直訳しただけのものなのでどうやったら SPIN-OUT のパズルを解くことができるか分かりづらいかもしれません。この説明書では主に SPIN-OUT と 2 進数との関係を元に SPIN-OUT を解こうとしています。実際に SPIN-OUT をやれば数と SPIN-OUT の動きとの関係がつながっていることを体感することができると思います。
なお、この SPIN-OUT もほかのパズルと同様に自作することができます。しかし、本物の SPIN-OUT から予想した設計図では、材料の切断に 0.5mm の精度が必要になり、よほどのカッターテクニック (ほぼ達人級) の持ち主でなければ、作ったときに誤差が生じてしまいます。なお、担当の学生が作成したときには 3 時間ぐらいはかかりました。このように SPIN-OUT の自作は万人向けではないのでここでは設計図を示しません。どうしても自作に挑戦してみたい人は所先生に頼んでみてください。
| 10進数 | 2進数 |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
みなさんが普段、日常で使っている数の多くは 10 進数です。10 進数とは、「0」から「9」までの 10 個の数字で数を表したもので、 10 個の数字で数を表す方法を 10 進法と言います。この 10 進数は 0 から順に 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 と増え、その後 10 になります。10 個の数字を使い切った後は位を増やすことによって数を表すことができます。
今、「2731」という 10 進数を例に考えてみます。「2731」とは、1000 が 2 個,100 が 7 個、10 が 3 個、1 が 1 個集まった数です。よって
2731 = 1000×2 + 100×7 + 10×3 + 1×1
と表せます。また、1000 = 103, 100 = 102, 10 = 101, 1 = 100 と書き換えることができます。
2 進数とは、「0」と「1」の 2 個の数字で表した数です。2 個の数字で表す方法を2 進法と言います。2 進数は,2 個の数字で数を表すため0, 1 の次は 10 になります。ここで、10 進数と 2 進数の対応表を示します。
10 進数で「2731」を表したときと同様にして、2進数の「5」を表すと、
5 = 22×1 + 21×0 + 20×1
となります。少しわかりづらいかと思いますが、10 進数では各桁が 10 の n−1 乗を表しているのに対し、2 進数では各桁が 2 の n−1 乗を表しています。2 進数では、数字が 2 つからなることが電子回路の ON/OFF と対応させることができるので、コンピュータ内部ではすべての数字を 2 進数に置き換えて処理しています。